Question

Maggie was on a long 209 mile road trip. The first part of the trip there was lots of traffic, she only averaged 20 mph. The second part of the trip there was no traffic so she could drive 43 mph. If the trip took her 7 hours, how long did she travel at each speed? In traffic she drove for hours After the traffic cleared she drove for hours.

Answer 1

We can solve this problem by setting up a system of equations.

We let x be the time Maggie traveled when there is traffic and let y be the time Maggie traveled when there is no traffic. The sum of these will be equal to 7 hours, represented in the equation as

`x+y=7`

When we multiply the time and the speed, we get the distance. Since we already defined variables x and y as time, we multiply the speed indicated in the problem with respect to the assigned variables for them. The distance travelled is equal to 209. We have the equation set-up as

`20x+43y=209`

Hence, we have the system of equations written as

`\begin{gathered} x+y=7 \\ 20x+43y=209 \end{gathered}`

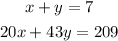
We use the elimination method to solve for the value of y. We multiply the first equation by -20. We have

`\begin{gathered} -20x-20y=-140 \\ 20x+43y=209 \end{gathered}`

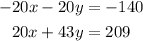
Solve for y

`\begin{gathered} 23y=69 \\ y=3 \end{gathered}`

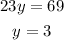
Use this value of y to solve the value of x using the first equation. We have

`\begin{gathered} x+3=7 \\ x=7-3 \\ x=4 \end{gathered}`

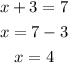
As we stated above, x represents the time Maggie traveled in traffic while y represents the time Maggie traveled in no traffic.

Therefore, it took Maggie 4 hours to drive while in traffic. Also, she drove for 3 hours after the traffic was cleared.