Question

One month Omar rented 9 movies and 7 video games for a total of $ 72. The next month he rented 3 movies and 5 video games for a total of $ 42 . Find the rental cost for each movie and each video game.

Answer 1

The cost for renting each movie is $2.75 and the cost for renting each video game is $6.75

EXPLANATION;

Given that

The cost of renting 9 movies and 7 video games is $72

The cost of renting 3 movies and 5 video games is $42

Follow the steps below to find the cost of each movie and video game

Step 1; Assign variables to the movie and video game

Let x represents the cost of each movie

Let y represents the cost of each video game

Step 2: Establish the system of equation

`\begin{gathered} \text{ 9x + 7y = 72 -------- equation 1} \\ \text{ 3x + 5y = 42 -------- equation 2} \end{gathered}`

Step 3; Slve the above equation simultaneously using elimination method

Firstly, we need to eliminate one of the variable before we can determine the other variable

Eliminate variable x by multiplying equation 1 by 1 and equation 2 by 3

`\begin{gathered} \text{ 9x + 7y = 72 }*\text{ 1} \\ \text{ 3x + 5y = 42 }*\text{ 3} \\ \\ \text{ 9x + 7y = 72--------- equation 3} \\ \text{ 9x + 15y = 126 ------- equation 4} \end{gathered}`

Subtract equation 4 from equation 3

`\begin{gathered} \text{ \lparen9x - 9x\rparen + \lparen7y - 15y\rparen = \lparen72 - 126\rparen} \\ \text{ 0 + \lparen-8y\rparen = -54} \\ \text{ -8y = -54} \\ \text{ Divide both sides by -8} \\ \text{ y = }\frac{\text{ -54}}{\text{ -8}} \\ \text{ y = \$6.75} \end{gathered}`

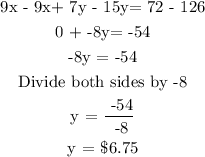
Find the value of x by substituting y = 6.75 in equation 1

`\begin{gathered} \text{ 9x + 7y = 72} \\ \text{ 9x + 7\lparen6.75\rparen = 72} \\ \text{ 9x + 47.25 = 72} \\ \text{ Subtract 47.25 from both sides of the equation} \\ \text{ 9x + 47.25 - 47.25 = 72 - 47.25} \\ \text{ 9x = 24.75} \\ \text{ Divide both sides by 9} \\ \text{ x = }\frac{\text{ 24.75}}{\text{ 9}} \\ \text{ x = \$2.75} \end{gathered}`

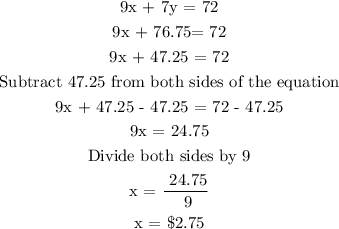
Therefore, the cost for renting each movie is $2.75 and the cost for renting each video game is $6.75