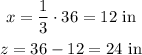Question

A builder is installing hardwood flooring. He has to cut a 72 inch piece into three separate pieces so that the smaller piece is one third the length of the longest piece, and the third piece is 12 inches shorter than the longest. How long is each piece?

Answer 1

Smallest piece = 12 in

Longest piece = 36 in

Third piece = 24 in

Explanation:

We have the following:

Let x = smallest piece

Let y = longest piece

Let z = third piece

We can propose the following system of equations:

`\begin{gathered} x+y+z=72\text{ (1)} \\ x=(1)/(3)y\text{ (2)} \\ z=y-12\text{ (3)} \end{gathered}`

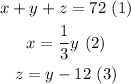
We replace equations 2 and 3 in 1, and solving for y:

`\begin{gathered} (1)/(3)y+y+y-12=72 \\ (1)/(3)y+2y=72+12 \\ y+3\cdot2y=3\cdot84 \\ 7y=252 \\ y=(252)/(7) \\ y=36\text{ in} \end{gathered}`

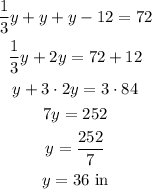
Now, for x and y:

`\begin{gathered} x=(1)/(3)\cdot36=12\text{ in} \\ z=36-12=24\text{ in} \end{gathered}`