Two lines are perpendicular if the product of their slopes is -1.
When the variable y is isolated and the expressions are reduced to its lowest terms, the coefficient of the variable x corresponds to the slope of the line.
Isolate y from both equations to find if the lines are perpendicular or not.
First expression:
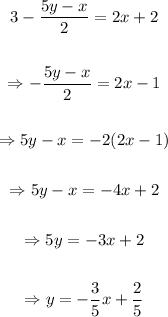
Second expression:
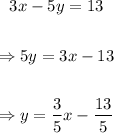
The slope of the first line is -3/5 and the slope of the second line is 3/5. The product of the slopes is:

Which is not equal to -1.
Therefore, the lines are not perpendicular.