Substituting v₀=180 and h(t)=440 in the given equation we get:
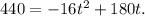
Subtracting 440 from the above equation we get:
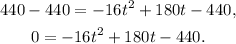
Dividing the above equation by -2 we get:
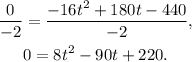
Using the quadratic formula for second-degree equations we get:
![\begin{gathered} t=\frac{-(-90_{})\pm\sqrt[]{(-90)^2-4(8)(220)}}{2\cdot8}, \\ t=\frac{90\pm\sqrt[]{8100-7040}}{16}, \\ t=\frac{90\pm\sqrt[]{1060}}{16}, \\ t=\frac{90\pm2\sqrt[]{265}}{16}, \\ t=\frac{45\pm\sqrt[]{265}}{8}\text{.} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/l9r1g34rjp6l8hjg5bqg5exdkuf1ork5q2.png)
Therefore, the firework will reach a height of 440 feer after
![\begin{gathered} t=\frac{45-\sqrt[]{265}}{8}\approx(45-16.2788208)/(8) \\ =(28.7211794)/(8)=3.590147425\approx3.6. \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2xpfgma24iu0f30ltqv2d1a155byk5ezri.png)
seconds.
Answer: 3.6.
The number without being rounded yet is 3.590147425.