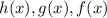SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the formula for the rate of change
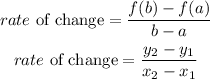
STEP 2: Write the given intervals
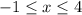
STEP 3: Find the average rate of change of f(x)
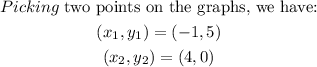
We substitute the coordinates into the rate of change formula:

STEP 4: Find the rate of change of g(x)
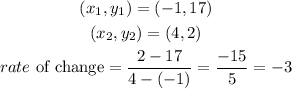
STEP 5: Find the rate of change of h(x)
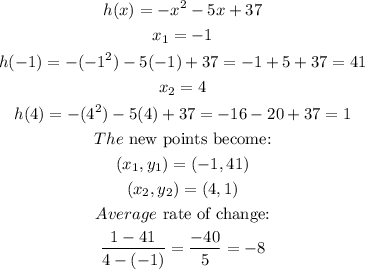
STEP 6: Write the average rates of change for the functions
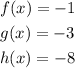
The average rates of change in ascending order will be -8,-3,-1
Hence, the arrangement of the functions according to their ascending order of average rates of changes are: