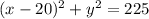Given
An inground sprinkler nozzle sprays water onto the grass in the shape of a circle, with the nozzle at the center of the circle.
On the coordinate plane, the nozzle is located at (20, 0) and the points (35, 0) and (5, 0) lie on the circle.
To find:
Which equation represents the boundary that the sprinkler covers?
Step-by-step explanation:
It is given that,
The nozzle is located at (20,0).
Then,
The equation of the circle is given by,
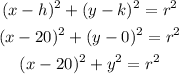
Since,
The distance between any point on the circle and the centre is known as radius.
Then,
The radius is given by,
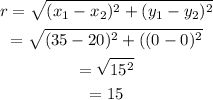
Therefore,
The equation of the circle is,
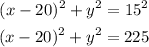
Hence, the answer is option A),