Question

A concave mirror has a radius of curvature of 20.0 cm. Locate the image for an object distance of 40.0 cm. Indicate whether the image is real or virtual, enlarged or diminished, and upright or inverted.

Answer 1

Given:

the radius of the curvature of concave mirror is

`R=-\text{ 20 cm}`

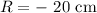
The distance of the object is,

`d_0=-40\text{ cm}`

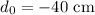
Required:

find the distance of the image.

Step-by-step explanation:

we know that, radius of curvature is given by,

`f=(R)/(2)`

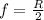
Plugging the value of R in the above formula , we get:

`\begin{gathered} f=\frac{-20\text{ cm}}{2} \\ f=-10\text{ cm} \end{gathered}`

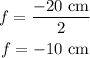
now from the mirror formula,

`(1)/(f)=(1)/(d_0)+(1)/(d_i)`

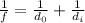
Plugging all the values in the above formula, we get:

`\frac{1}{-10\text{ cm}}=(1)/(d_i)+\frac{1}{-40\text{ cm}}`

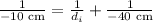
solve for di, we get:

`\begin{gathered} (1)/(d_i)=\frac{1}{40\text{ cm}}-\frac{1}{10\text{ cm}} \\ d_i=-(40)/(3) \\ d_i=-13.33\text{ cm} \end{gathered}`

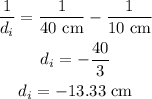
Thus, the distance of the image is 1

`13.33\text{ cm.}`

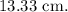
we can see that image distance is negative, so that means the image formed in front of the mirror. The image is real.

now we calculate the magnification.

`\begin{gathered} m=-(d_i)/(d_0) \\ m=-\frac{-13.33\text{ cm}}{-40\text{ cm.}} \\ m=-0.33 \end{gathered}`

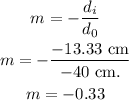
we can see that m is negative which means, the image is diminished and the image is inverted.

Final answer: the distance of the image is 13.33 cm. the image is real, diminished, and inverted.