Question

Find the upper limit of the outlier of the following box and whisker plot.

Answer 1

Consider that the given box and whisker plot lies in the interval,

`20\leq x\leq75`

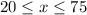
These end points are referred as the Outliers of the plot.

The interquartile range (IQR) of the given plot is,

`\text{IQR}=65-38=27`

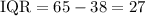
The upper limit of the outlier is given by,

`=Q_3+1.5(IQR)`

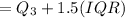
Substitute the values and simplify,

`\begin{gathered} \text{ Upper Limit of Outlier}=Q_3+1.5(IQR)\text{ } \\ \text{ Upper Limit of Outlier}=65+1.5(27) \\ \text{ Upper Limit of Outlier}=65+40.5 \\ \text{ Upper Limit of Outlier}=105.5 \end{gathered}`

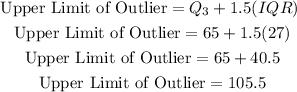
Therefore, the correct option should be the 2nd option, as it is closest to the answer.