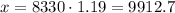Answer
• At the end of the first year, we will have $8,330.
,
• At the end of the second year, we will have $9912.7.
Step-by-step explanation
Given
• $7000 is placed
,
• Pays 19% interest compounded each year.
Procedure
If we place $7000, we could consider that this is our 100% (1). Thus, at the end of the first year, we will have 119% (1.19). Making a relation that represents the latter we can find the total amount at the end of 1 year:
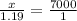
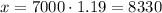
Now, considering that $8330 is our 100% (1) and the amount in the account at the end of 2 years is 119% (1.19), then, following the same procedure: