Given:
Magnitude of vector A = 10.0 m
Magnitude of vector B = 20.0 m
Magnitude of vector C = 7.0 m
Let's find the magnitude and direction of the net displacement using the component method of vector addition.
The vector of magnitude r which makes an angle θ with the positive x-axis in vector form is:
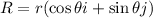
Vector A:
From the figure, vector A makes an angle of -90° with the x-axis, thus, we have:
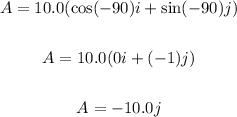
Vector B:
Vector B makes an angle of 45° with a magnitude of 20.0 m. Thus, we have:
![\begin{gathered} B=20.0(\cos 45i+\sin 45i) \\ \\ B=20.0(0.5\sqrt[]{2}i+0.5\sqrt[]{2}j) \\ \\ B=10.0\sqrt[]{2i}+10\sqrt[]{2}j \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/7zyjdyj05kyf5u5er6qtgllb55gg8vj3ba.png)
Vector C:
Vector C makes an angle of -30° with a magnitude of 7.0 m. Thus, we have:
![\begin{gathered} C=7.0(\cos (-30)i+\sin (-30)j) \\ \\ C=3.5\sqrt[]{3}i+3.5j \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/apc1009bv02wpn58ti1nfcv2u6ioyr3ivk.png)
To find the net displacement, apply the formula:
Net displacement = A + B + C
Hence, we have the net diplacement below:
![\begin{gathered} A+B+C \\ \\ (-10.0j)+(10.0\sqrt[]{2}i+10.0\sqrt[]{2}j)+(3.5\sqrt[]{3}i+3.5j) \\ \\ =10.0\sqrt[]{2}i+3.5\sqrt[]{3}i-10.0j+10.0\sqrt[]{2}j+3.5j \\ \\ =20.202i+0.642j \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/yfhw5mrxqhtcsl4hcnttylgmzzs7uowl83.png)
To find the magnitude of the net displacement, we have:
![\begin{gathered} \text{ magnitude=}\sqrt[]{20.202^2+0.642^2} \\ \\ \text{ magnitude=}\sqrt[]{408.12+0.412} \\ \\ \text{magnitude = }\sqrt[]{408.53} \\ \\ \text{magnitude = }20.212 \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/o3dqtm2738yl3jlov1k1iaea537wmkvo0w.png)
To find the direction, we have:
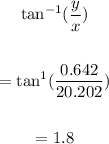
Therefore, the magnitude of the net displacement is 20.21 m while the direction is at 1.8 degrees.
ANSWER:
Magnitude = 20.21 m
Direction = 1.8°