Given Data:
The given side length of a square is: x
The length of the rectangle is 4 yadr grater than the square. Thus, the length of the rectangle is: x+4
The width of the rectangle is 2 yard less than the square. Thus, the width of the rectangle is: x-2.
The expression to calculate the area of the square is,
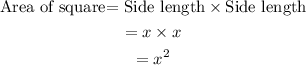
The expression to calculate the area of the rectangle is,
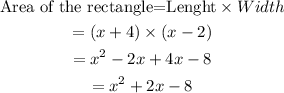
Given the area of the square ane the rectangle are same.
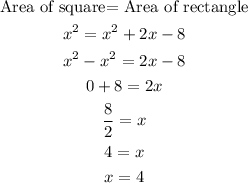
The lenght of th square is x=4
Substitute x=4 in the expresso=ion to calculate the length of the rectangl.

Thus, the lenght of the rectangular rug is 8.