Question

on a certain hot summer day 629 people use the public swimming pool The daily prices are $1.25 for children and $2.50 for adults The receptionist for admission totaled $1,200 how many children and how many adults swim at the public pool that day

Answer 1

Let the number of children be "c" and the number of adults be "a".

There are a total of 629 adults and children.

Thus, we can write an equation:

`c+a=629`

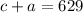
Price of each children admit is 1.25 and each child admit is 2.50 for a total of $1200.

Thus, we can write an equation to represent this information as:

`1.25c+2.50a=1200`

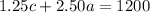
We can solve the system of 2 equations we got and find out the values of "a" and "c".

Solving the first equation for c:

`\begin{gathered} c+a=629 \\ c=629-a \end{gathered}`

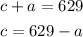
We substitute it into second equation and figure out a:

`\begin{gathered} 1.25c+2.50a=1200 \\ 1.25(629-a)+2.50a=1200 \\ 786.25-1.25a+2.50a=1200 \\ 1.25a=1200-768.25 \\ 1.25a=413.75 \\ a=(413.75)/(1.25) \\ a=331 \end{gathered}`

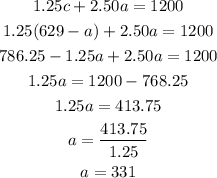
Now, we simply find out c:

`\begin{gathered} c=629-a \\ c=629-331 \\ c=298 \end{gathered}`

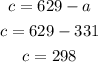
Answer:

Children = 298Adults = 331