Let us plot the graph of this to get a clearer insight.
From the diagram shown above, we have to find the lengths AC, AB, and BC using the distance between two points.
Distance between two points is given by the formula:
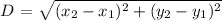
Based on the above formula:
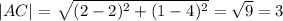
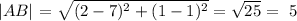
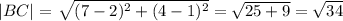
For the set of coordinates to form a right angled triangle, the pythagora's theorem must be obeyed, that is:
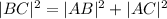
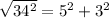
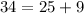
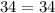
Since the Right Hand Side equals the Left Hand Side, Pythagoras theorem is obeyed, and the set of coordinates form a right angled triangle.