Question

Use slope to determine if lines AB and CD are parallel, perpendicular, or neither 6. 4(-3, 8), B(3, 2), C(7, 1), D(5,-1)m(AB) m(CD)Types of Lines

Answer 1

Note:

1. Condition for paralleleism of lines AB and CD

m(AB) = m(CD)

That is both lines AB and CD have equal slopes

2. Condition for perpendicularity of lines AB and CD

m(AB) = -1 / m(CD)

The slope of a line is calculated by using the formula:

`m\text{ = }(y_2-y_1)/(x_2-x_1)`

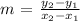
Let us calculate the slopes of lines AB and CD and see which of the two conditions above is met.

For line AB:

A(-3, 8) and B(3, 2)

`\begin{gathered} m(AB)\text{ = }(2-8)/(3-(-3)) \\ m(AB)\text{ = }(-6)/(6) \\ m(AB)\text{ = -1} \end{gathered}`

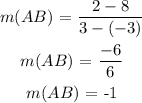
For line CD:

C(7, 1) and D(5, -1)

`\begin{gathered} m(CD)\text{ = }(-1-1)/(5-7) \\ m(CD)\text{ = }(-2)/(-2) \\ m(CD)\text{ = 1} \end{gathered}`

You would see that m(AB) = -1