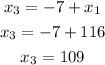Question

Can you please help You can solve a different way than indicated.

Answer 1

x1 = 116

x2 = 227

x3 = 109

EXPLANATION :

From the problem, with k1 = 5, k2 = -6 and k3 = -7

`\begin{gathered} Eq.1:2x_1-x_2=5 \\ \\ Eq.2:16x_1-x_2-15x_3=-6 \\ \\ Eq.3:-x_1+x_3=-7 \end{gathered}`

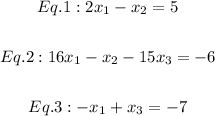
We have 3 equations.

Our goal is to have an equation with 1 variable only.

By substitution method :

Express Eq.1 as x2 in terms of x1 and label it as Eq.4

`\begin{gathered} 2x_1-x_2=5 \\ -x_2=5-2x_1 \\ x_2=2x_1-5 \\ \text{ The new equation will be :} \\ \\ Eq.4:x_2=2x_1-5 \end{gathered}`

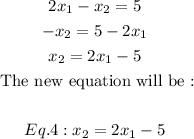
Express Eq.3 as x3 in terms of x1 and label it as Eq.5

`\begin{gathered} -x_1+x_3=-7 \\ x_3=-7+x_1 \\ \text{ The new equation will be :} \\ \\ Eq.5:x_3=-7+x_1 \end{gathered}`

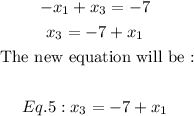
Now, substitute Eq.4 and Eq.5 to Eq.2, so we will only have the variable x1

`\begin{gathered} 16x_1-x_2-15x_3=-6 \\ 16x_1-(2x_1-5)-15(-7+x_1)=-6 \\ 16x_1-2x_1+5+105-15x_1=-6 \\ -x_1+110=-6 \\ -x_1=-6-110 \\ -x_1=-116 \\ x_1=116 \end{gathered}`

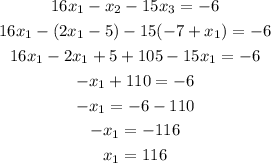
We now have the value of x1 which is 116.

Substitute x1 = 116 to Eq.4 to get the value of x2 :

`\begin{gathered} x_2=2x_1-5 \\ x_2=2(116)-5 \\ x_2=232-5 \\ x_2=227 \end{gathered}`

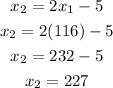
Substitute x1 = 116 to Eq.5 to get the value of x3 :

`\begin{gathered} x_3=-7+x_1 \\ x_3=-7+116 \\ x_3=109 \end{gathered}`