Question

Compare and contrast the following functions. Observations an include: increasing, decreasing, growthrate, starting value, linear, exponential, etc.Function 1: y = 200 (1/4) ^xFunction 2: y = 3x + 200Similarities:Differences:

Answer 1

We have here two different functions. One case represents an exponential function, and the other case is a linear function.

The exponential function is:

`y=200((1)/(4))^x`

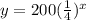
The linear function is:

`y=3x+200`

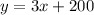
We can check both functions graphically as follows:

1. The exponential function can be represented as:

2. The linear function can be seen as follows:

Similarities between functions

Both functions have the same y-intercept value. If we substitute x = 0 in both functions, we have a value of 200 for both functions:

`\begin{gathered} f(x)=200((1)/(4))^x\Rightarrow200((1)/(4))^0=200 \\ g(x)=3x+200\Rightarrow3(0)+200=200 \end{gathered}`

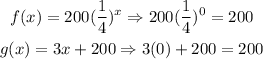
And if we say that the starting value is x = 0, then both functions have the same starting value, y = 200.

Therefore, they have the same starting value.

Differences between functions

1. The linear function is increasing constantly, at a rate given by m = 3. It has a positive slope, m = 3.

The exponential function is decreasing constantly at a rate given by the fraction 1/4. When we have an exponential with a fractional factor raised to the independent variable, x, then the exponential function is decreasing.

2. The growth rate for the linear function is given by its slope, m = 3. It is a positive growth rate, and we can say that for any "run" on the x-axis, we have a "rise" of 3 units on the y-axis. The exponential function has a decay rate, and it is doing that by rising the constant factor, 1/4, to any value of x. As we can see from the graph, the function has an asymptotic behavior as the function tends to infinity, that is, the function tends to have a value of y = 0 as it tends to infinity.

Additionally, if we know that the general case of the exponential function is given by:

`\begin{gathered} y=ab^x \\ b=1-r \\ \text{ In this case, we have:} \\ (1)/(4)=1-r\Rightarrow r+(1)/(4)=1-r+r=r+(1)/(4)=1 \\ r=1-(1)/(4)=(4)/(4)-(1)/(4)=(3)/(4)=0.75 \\ \end{gathered}`

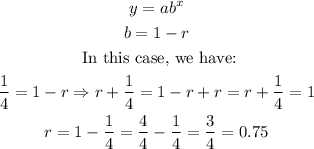
That is, the decay rate is 0.75 (or 75/100 = 75%).

3. As we said above, Function 1 is a case of the exponential function, while Function 2 is a case of a linear function.

Therefore, in summary, we have that:

Similarities:

• Both functions have the same starting value, when x = 0, both functions have y = 200 (the same y-intercept value).

Differences:

• Function 1 is a case of the exponential function. Function 2 is a case of a linear function.

,

• Function 1 is ,decreasing at a decay rate of 75% (r is negative, 0.75),, and we can say that this function is always decreasing. ,Function 2 is increasing constantly at a slope of m = 3, (we can say that for any "run" on the x-axis, we have a "rise" of 3 units on the y-axis). This is a constant growth rate (m = 3), and we can say that this linear function is increasing constantly.

,

• Function 1 has an asymptotic behavior as it tends to positive infinity, and the asymptote is equal to y = 0.