Question

Divide using long division. Check your answer. (5x^2-3x+2) / (x-1) The quotient is _____ with remainder _____.

Answer 1

Long Division of Polynomials

Divide:

`5x^2-3x+2\text{ by }x-1`

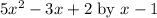
Arranging dividend and divisor for the long division procedure:r thefrrrArA

`x-1\text{ \mid 5}x^2-3x+2`

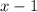
Divide the first term of the dividend by the first term of the divisor:of the d

`(5x^2)/(x)=5x`

Multiply 5x by the divisor: div

`5x*(x-1)=5x^2-5x`

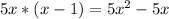
Subtract this product from the dividend:

`\begin{gathered} \text{ }5x \\ x-1\text{ \mid }5x^2-3x+2 \\ \text{ }5x^2-5x \\ \text{ }2x+2 \end{gathered}`

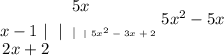
Now divide 2x+2 by x = 2. Repeat the procedure:rocedurrocedu

`\begin{gathered} \text{ }5x+2 \\ x-1\text{ \mid }5x^2-3x+2 \\ \text{ }5x^2-5x \\ \text{ }2x+2 \\ \text{ }2x-2 \\ \text{ 4} \end{gathered}`

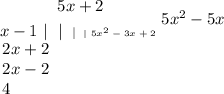
The quotient is 5x + 2 and the remainder is 4

a