Question

Reiko needs to mail her Christmas cards and packages and wants to keep her mailing costs to no more than $360.00. The number of cards is at least 22 more than twice the number of packages. The cost of mailing a card (with pictures enclosed) is $3.00 and for a package the cost is $6.00.Write a system of 2 inequalities to model this situation. Use "x" for the number of packages and " y" for the number of cards.

Answer 1

The first step to solving this problem is to interprete the sentence and write it using inequality symbols.

Mailing cost should be no more than $360

`\text{Mailing Cost }\leq\text{ 360}`

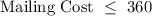
The number of cards is at least 22 more than twice the number of packages

x represents the number of packages and y the number of cards:

`y\text{ }\ge\text{ 22 + 2x}`

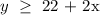
Cost of a package is $6 and that of a card is $3

`6x\text{ + 3y }\leq\text{ 360}`

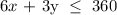
Answer:

First Inequality:

`6x\text{ + 3y }\leq\text{ 360}`

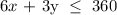
Second inequality:

`y\text{ }\ge\text{ 22+ 2x}`

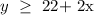
Using a graphing tool, the graphs of the inequality is shown below:

The region of overlap is the required solution. The value combinations in this region would meet the constraints

Will 20 packages and 26 cards meet the cost and number requirements?

The point (20, 26) does not lie in the region of solution.

Answer: No

Will 40 packages and 36 cards meet the cost and number requirement?

The point (40, 36) does not lie in the region of solution

Answer : No