Question

TRUE OR FALSE PHOTO ATTACHED THANK YOU QUWESTION 215N THIS IS NOT FROM GRAD3D ASSIGNE,MNT

Answer 1

Given:

`\begin{gathered} P=\text{ \$2000} \\ r=2\text{ \%=}(2)/(100)=0.02 \\ n=12\text{ times (monthly compounding)} \\ t=1\text{year} \end{gathered}`

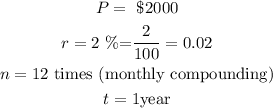
When compounded monthly:

Using the compound interest formula;

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ A=2000(1+(0.02)/(12))^(12*1) \\ A=\text{ \$2040.37} \\ \\ \\ \\ \text{The interest made is;} \\ I=A-P \\ I=2040.37-2000 \\ I=\text{ \$40.37} \\ \\ To\text{ the nearest whole number,} \\ I\approx\text{ \$40} \end{gathered}`

When compounded weekly:

n = 52 times (assume 52 weeks make 1 year)

Using the compound interest formula;

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ A=2000(1+(0.02)/(52))^(52*1) \\ A=\text{ \$2040.3}9 \\ \\ \\ \\ \text{The interest made is;} \\ I=A-P \\ I=2040.39-2000 \\ I=\text{ \$40.3}9 \\ \\ To\text{ the nearest whole number,} \\ I\approx\text{ \$40} \end{gathered}`

From the calculations made for monthly and weekly compounding, it can be seen that the interest made in both cases is approximately equal.

Hence, $2000 invested at 2% compounded monthly DOES NOT earn more interest in a year than the same amount invested at 2% compounded weekly.

Therefore, the statement is FALSE.