The expression will be undefined if the denominator will be equal to 0.
From the given expression :
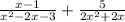
If any of the denominator equal to 0, the expression will be undefined
Let's find the value of x that will make the first fraction undefined.
The denominator of the first term is :
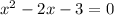
Using factoring :
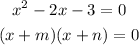
We need to think of two numbers, m and n that has a product of -3 and a sum of -2
in this case, m must be -3 and n must be 1.
The sum is -2 and the product is -3
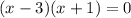
Then find the value of x by equating the factors to 0 :

So the values of x that will make the first fraction undefined are -1 and 3
Next is to find the values of x to make the 2nd fraction undefined
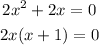
Then equate both factors to 0.
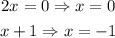
The values of x that will make the 2nd fraction undefined are 0 and -1
To summarize :
The values of x that will make the whole expression undefined are :
-1, 3 and 0