Question

Hint: Work the problem in metric units (m, m/s and m/s2) and then convert the initial speed from m/s to mph. Speeds that are greater than the critical speed you calculated are safe, because they cause the firework to safely explode higher than the critical height. We do NOT want the firework to explode too close to the ground!

Answer 1

The kinetic energy of the firework when it is launched is,

`K=(1)/(2)mv^2`

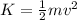
At the minimum height the potential energy of the firework is,

`U=\text{mgh}`

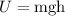
At the height the kinetic energy is converted into potential energy therefore, according to conservation of energy,

`K=U`

Plug in the known values,

`\begin{gathered} (1)/(2)mv^2=mgh \\ v^2=2gh \\ v=\sqrt[]{2gh} \end{gathered}`

Substituting values,

`\begin{gathered} v=\sqrt[]{2(9.8m/s^2_{})(240\text{ m)}} \\ =(68.6\text{ m/s)}(\frac{2.24\text{ mph}}{1\text{ m/s}}) \\ \approx153.7\text{ mph} \end{gathered}`

Therefore, the launch speed of the firework is 153.7 mph.

As the launch speed is approximately equal to 160 mph therefore, the firework can be launched safely with speed 160 mph.