Question

How many liters each of a 35 % acid solution and a 85 % acid solution must be used to produce 90 liters of a 60 % acidsolution? (Round to two decimal places if necessary.)

Answer 1

`45liters`

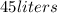
1) This is a problem of rational equations, so let's set them so that we can solve it:

`0.35x+0.85\left(90-x\right?=0.6*90`

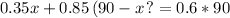
Note that on the left we have the mixture, 35% = 0.35 of a solution +0.85 times the number of liters we want to produce minus x. This is going to be equal to 60% (0.6) times 90.

2) Now, we can solve it:

`\begin{gathered} 0.35x+0.85\left(90-x\right)=0.6\cdot \:90 \\ 0.35x+0.85\left(90-x\right)=54 \\ 0.35x\cdot \:100+0.85\left(90-x\right)\cdot \:100=54\cdot \:100 \\ 35x+85\left(90-x\right)=5400 \\ -50x+7650=5400 \\ -50x=-2250 \\ (-50x)/(-50)=(-2250)/(-50) \\ x=45 \end{gathered}`

Once the hardest part is done, we had to deal with the good old Algebra.