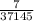Question

14. A jury pool consists of 26 people, 16 men, and 10 women. Compute the probability that a randomly selected jury of 12 people is all male.

Answer 1

Consider that the number of selections possible from 'n' distinct objects taken 'r' at a time is given by the formula,

`^nC_r=(n!)/(r!\cdot(n-r)!)`

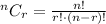
As per the given problem, there are 26 people consisting 16 men and 10 women.

Then, the number of ways to select a jury of 12 people is calculated as,

`\begin{gathered} =^(26)C_(12) \\ =(26!)/(12!\cdot(26-12)!) \\ =(26!)/(12!\cdot14!) \end{gathered}`

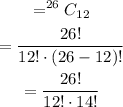
Similarly, the number of ways to select a jury of 12 men is calculated as,

`\begin{gathered} =^(16)C_(12) \\ =(16!)/(12!\cdot(16-12)!) \\ =(16!)/(12!\cdot4!) \end{gathered}`

The probability of an event is given by,

`\text{Probability}=\frac{\text{ Number of favourable outcomes}}{\text{Number of total outcomes}}`

So the probability that the jury contains all 12 males is calculated as,

`\begin{gathered} P(\text{all males})=\frac{\text{ No. of ways of selecting jury containing all males}}{\text{ Total no. of ways of selecting the jury }} \\ P(\text{all males})=(((16!)/(12!\cdot4!)))/(((26!)/(12!\cdot14!))) \\ P(\text{all males})=(16!)/(12!\cdot4!)\cdot(12!\cdot14!)/(26!) \\ P(\text{all males})=(16!)/(4!)\cdot(14!)/(26!) \\ P(\text{all males})=(7)/(37145) \end{gathered}`

Thus, the required probability is obtained as,

`(7)/(37145)`