Question

12) Determine the area of the shaded region. The vertices of the triangle are the centers of the arcs.

Answer 1

Step-by-step explanation

Step 1: We find the area of the triangle. The given triangle is equilateral, and the formula to find the area of an equilateral triangle is:

`A=(√(3))/(4)a^2`

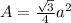
Then, we have:

`\begin{gathered} a=5+5=10 \\ A=(3)/(4)a^(2) \\ A=(3)/(4)(10)^2 \\ A=(3)/(4)(100) \\ A=(300)/(4) \\ A=75 \end{gathered}`

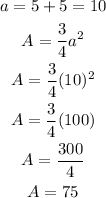
Step 2: We find the area of a sector of the circle. The formula to find the area of a sector of a circle is:

`\begin{gathered} \text{ Area of a sector of a circle }=(\theta)/(360\degree)\cdot\pi r \\ \text{ Where} \\ \theta\text{ is the angle measured in degrees} \\ \text{r is the radius of the circle} \end{gathered}`

Then, we have:

`\begin{gathered} \theta=60° \\ \text{ Area of a sector of circle }=(\theta)/(360\degree)\cdot\pi r \\ \text{ Area of a sector of circle }=(60°)/(360°)\cdot\pi(5) \\ \text{ Area of a sector of circle }=((1)/(6))\pi(5) \\ \text{ Area of a sector of circle }=(5\pi)/(6) \\ \text{ or} \\ \text{ Area of a sector of circle }\approx2.62 \end{gathered}`

Step 3: We find the area of the shaded region.

`\begin{gathered} \text{ Area of shaded region }=\text{ Area triangle}-3\cdot\text{ Area of a sector of circle} \\ \text{ Area of shaded region }=75-3\cdot(5\pi)/(6) \\ \text{ Area of shaded region }\approx75-7.85 \\ \text{ Area of shaded region }\approx67.15 \end{gathered}`Answer

The area of the shaded region is approximately 67.15 square units.