Question

There are two similar cones. Cone A has an altitude of 5 cm and Cone B has analtitude of 13 cm.If Cone A weighs 20 lbs, how much does Cone B weigh?Enter your answer in decimal form. Do not round.

Answer 1

First cone: h=5cm

Second cone: h=13cm

They are similar!

Since they are similar, the radius and height are also similar.

Therefore:

`(h_1)/(r_1)=(h_2)/(r_2)`

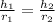
Replacing:

`\begin{gathered} (5)/(r_1)=(13)/(r_2) \\ r_25=13r_1 \\ r_2=(13)/(5)r_1 \end{gathered}`

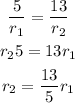
Now, the volume of a cone is given by:

`\begin{gathered} V_1=(\pi *r_1^2*h_1)/(3) \\ V_2=(\pi(r_2)^2h_2)/(3) \end{gathered}`

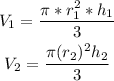
Dividing v1/v2:

`(V_1)/(V_2)=(\pi(r_(1))^(2)h_(1))/(3)*(3)/(\pi(r_2)^2h_2)`

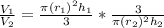
Solving:

`(V_1)/(V_2)=(r_1^2*5)/(r_2^2*15)`

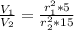
Substituing r2=(13/5)* r1

`(V_(1))/(V_(2))=(r_1^2*5)/(((13)/(5))^2*r_1^2*15)`

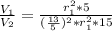
Simplifying:

`(V_1)/(V_2)=(5*5^2)/(13^2*15)=(125)/(2535)`

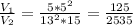
We can assign V1=20lb since the volume could represent weight if the material of both cones are uniform:

`\begin{gathered} (20)/(V_2)=(125)/(2535) \\ V_2=(20*2535)/(125)=405.6\text{ }lb \end{gathered}`

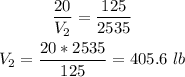
The asnwer is: The cone B weigh: 405.6 lb.