Answer:
d. -6
Step-by-step explanation:
By the remainder theorem, we get that:
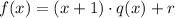
Where q(x) is another polynomial and r is the remainder.
To eliminate the value of q(x), we will replace x by -1 to get:
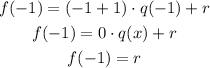
But f(x) = x^(88) + 5x - 2, so f(-1) will be equal to:
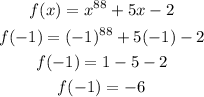
Therefore, if f(-1) = -6 and f(-1) = r, we get that
r = -6
So, the remainder is d. -6