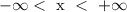Question

F(x) = \sqrt{x} - 6find the inverse of f(x) and its domain

Answer 1

`\begin{gathered} f^(-1)(x)=(x+6)^2 \\ \text{Domain =}-\infty<\text{ x }<\text{ +}\infty \end{gathered}`

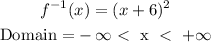
Step-by-step explanation

We want to find the inverse of:

`f(x)\text{ = }\sqrt[]{x}-\text{ 6}`

To do that, we will make f(x) to be y and make x the subject of the function:

`\begin{gathered} y\text{ = }\sqrt[]{x}\text{- 6} \\ \Rightarrow\text{ y + 6 = }\sqrt[]{x} \\ \text{Find the square of both sides:} \\ \Rightarrow x=(y+6)^2 \end{gathered}`

Now, x becomes f-1(x) and y becomes x:

`f^(-1)(x)=(x+6)^2`

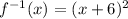
This is the inverse of the function f(x).

For the domain, we have to find the values of x such that the function can be valid.

There are no values of x that can cause the function to be invalid, so the domain is:

`-\infty<\text{ x }<\text{ +}\infty`