Question

miguel is designing shipping boxes that are rectangular prisms. the shape of one box, with height h in feet, has a volume defined by the function V(h)=h(h-10)(h-8). Graph the function. What is the maximum volume for the domain 0 < h< 10? Round to the nearest cubic foot.

Answer 1

105 ft^3

EXPLANATION :

From the problem, we have the volume function :

`V(h)=h(h-10)(h-8)`

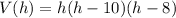
Expand the function :

`\begin{gathered} V(h)=h(h^2-18h+80) \\ V(h)=h^3-18h^2+80h \end{gathered}`

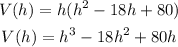
Get the first derivative of the function :

`V^(\prime)(h)=3h^2-36h+80`

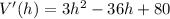
The maximum of the function is the value of h when V'(h) = 0.

That will be :

`0=3h^2-36h+80`

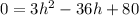
Using quadratic formula with a = 3, b = -36 and c = 80 :

`\begin{gathered} h=(-b\pm√(b^2-4ac))/(2a) \\ \\ h=(-(-36)\pm√((-36)^2-4(3)(80)))/(2(3)) \\ \\ h=(36\pm√(336))/(6) \\ \\ h=(36+√(336))/(6)=9.06 \\ \\ h=(36-√(336))/(6)=2.94 \end{gathered}`

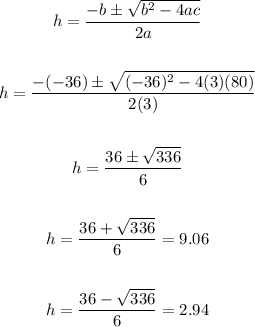
So we have two values of h, h = 9.06 and 2.94

We need to substitute these to the function and compare the resulting volumes.

`\begin{gathered} V(h)=h(h-10)(h-8) \\ V(9.06)=9.06(9.06-10)(9.06-8)=-9.03 \\ V(2.94)=2.94(2.94-10)(2.94-8)=105.03 \end{gathered}`

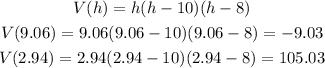
Since there's no negative volume. The volume is 105 ft^3

Graphing the function :

The zeros from the functions are (0, 0), (10, 0) and (8, 0)

The local minimum is (9.06, -9.03)

and the local maximum is (2.94, 105.03)