Question

Dilate Triangle ABC below using A as the center and a scale factor of 2. Leave all construction marks.AB=40 mmBC=20 mmAC=27 mm

Answer 1

Given:

AB=40 mm

BC=20 mm

AC=27 mm

The objective is to dilate triangle ABD with a scale factor of 2, using A as the centre.

Since, if A is used as center, then the remaining sides will get reduced by a factor of 2.

If AB=40mm,

`\begin{gathered} AB^(\prime)=(AB)/(Scalefactor) \\ AB^(\prime)=(40)/(2) \\ AB^(\prime)=20 \end{gathered}`

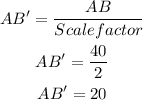
Similarly if BC=20 mm

`\begin{gathered} B^(\prime)C^(\prime)=\frac{BC}{Scale\text{ factor}} \\ B^(\prime)C^(\prime)=(20)/(2) \\ B^(\prime)C^(\prime)=10\text{ } \end{gathered}`

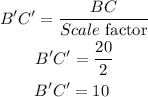
And if AC=27 mm

`\begin{gathered} AC^(\prime)=\frac{AC}{Scale\text{ factor}} \\ AC^(\prime)=(27)/(2) \\ AC^(\prime)=13.5 \end{gathered}`

If we construct the dilated triangle AB'C',

Hence, the required dilated triangle AB'C' has been obtained.