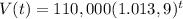SOLUTION:
Case: Exponential Equations
Exponentiation is a mathematical operation, written as bⁿ, involving two numbers, the base b, and the exponent or power n, and pronounced as "b raised to the power of n
Given:
In 1985, the house was valued at $110,000,
V(t)=?
1985 is the starting point, t=0
V(0)= $110,000
In 2005, the house was valued at $145,000,
2005 is the starting point, t=
V(20)= $145,000
Method:
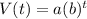
Step 1: Plug V(0)= $110,000
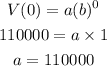
Step 2: Now we replace the value of a
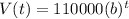
Step 3: Now we plug V(20)= $145,000
![\begin{gathered} V(20)=110000(b)^(20) \\ 145000=110,000(b)^(20) \\ Divide\text{ both sides by 110000} \\ 1.3181818=b^(20) \\ b=\sqrt[20]{1.3181818} \\ b=1.0139 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yqirx4wrlcv99ftcz7ycy7kx4b79jod81o.png)
Step 4: Therefore the model has the equation:
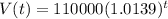
Final answer: