The pool is a box shape with width, length and depth. The volumen of the pool is:
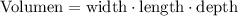
And the area is 761.76 square feet:
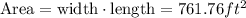
We also know the width is triple of depth and length is double of width, so:
![\begin{gathered} length=2\cdot\text{width} \\ \text{width}=3\cdot\text{depth}\Rightarrow\text{length}=2\cdot3\cdot\text{depth}=6\cdot\text{depth} \\ \text{Area}=761.76ft^2=width\cdot length=3\cdot depth\cdot6depth \\ 761.76=18\cdot depth^2 \\ depth^2=(761.76)/(18)=42.32\Rightarrow depth=\sqrt[]{42.32}\approx6.5\text{ ft} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/kel688rfdsk0ysj00thcmpes21etvlzpy7.png)
Now, we know the value of depth, so the width and length too.
So, we calculate the volumen:

The Volumen is 4943.25 cubic feet