Question

Check to see if I’m starting good and help to end

Answer 1

For this problem we have a certain function,

`MP(x)=xe^(-0.6x)`

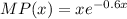
And we need to integrate it over the interal:

`0\le x\le100`

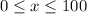
In order to solve this problem, we need to apply the integration by parts method. Such as:

`\int udv=uv-\int vdu`

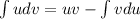
For our case we will call "u = x", therfore we have:

`\begin{gathered} u=x \\ (du)/(dx)=1 \\ du=dx \end{gathered}`

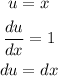
And the other part of the integral will be dv, we have:

`\begin{gathered} e^(-0.6x)dx=dv \\ \int e^(-0.6x)dx=\int dv \\ -1.67e^(-0.6x)=v \\ e^(-0.6x)=-(v)/(1.67) \\ e^(-0.6x)=-0.6v \end{gathered}`

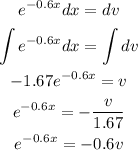
Using the second expression, we have:

`\begin{gathered} \int xe^(-0.6x)=-1.67xe^(-0.6x)+\int 1.67e^(-0.6x)dx \\ \int xe^(-0.6x)=-1.67xe^(-0.6x)-2.78e^(-0.6x)+K \end{gathered}`

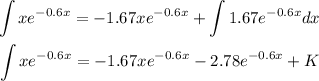
Now we need to apply the interval, to define the function:

`\begin{gathered} \int ^(100)_0xe^(-0.6x)=(-1.67xe^(-0.6x)-2.78e^(-0.6x))\begin{cases}100 \\ 0\end{cases} \\ \int ^(100)_0xe^(-0.6x)=(-1.67\cdot100\cdot e^(-0.6\cdot100)-2.78e^(-0.6\cdot100))-(-1.67\cdot0\cdot e^(-0.6\cdot0)-2.78e^(-0.6\cdot0)) \\ \int ^(100)_0xe^(-0.6x)=-167e^(-60)-2.78e^(-60)+2.78e^0 \\ \int ^(100)_0xe^(-0.6x)=2.78 \end{gathered}`

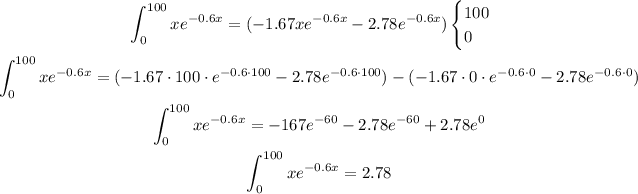
The value for the integral on the interval from 0 to 100 is 2.78.