Given:
There is a bag of coins containing $10 in coins.
The types are,
5 loonies ($1 coin),
10 quarters ($0.25),
20 dimes ($0.10) and
The rest are in nickels ($0.05).
Let the number of coins in nickel is x.
So that,
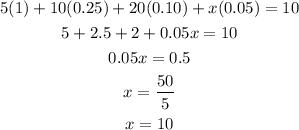
Therefore, the number of nickel coins is 10.
The total number of coins is 45.
(i) To find the probability that a chosen coin is $1 coin:
So, the answer is
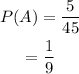
(ii) To find the probability that a chosen coin is $0.10 or $0.05 coin:
So, the answer is,
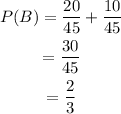
(iii) To find the probability that both the two chosen coin dimes coin( with replacement):
So, the answer is,
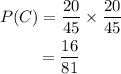
(iv) To find the probability that the first coin is a dollar ($1) and the second is a quarter ($0.25): (without replacement)
So, the answer is,
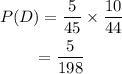
(v) To find the probability of drawing 2 coins that have a value of exactly $1.25:
So, the value is,
![undefined]()