1 Answer

Dimka · Answer 1 · 2023-09-09T19:41:49+0000

The Solution.

The given equation of a circle is

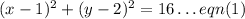
$(x-1)^2+(y-2)^2=16\ldots eqn(1)$

By formula, the equation of a circle is

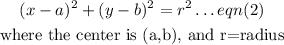
$\begin{gathered} (x-a)^2+(y-b)^2=r^2\ldots eqn(2) \\ \text{where the center is (a,b), and r=radius} \end{gathered}$

Comparing the corresponding terms in eqn(1) and eqn(2), we have

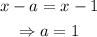
$\begin{gathered} x-a=x-1 \\ \Rightarrow a=1 \end{gathered}$

Similarly,

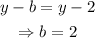
$\begin{gathered} y-b=y-2 \\ \Rightarrow b=2 \end{gathered}$

Also,

$\begin{gathered} r^2=16 \\ r=\sqrt[]{16}=\pm4 \\ r=\text{ +4 units ( -4 is discarded)} \end{gathered}$

Hence, the center of the circle is (1,2) while the radius of the circle is 4 units.

Please log in or register to add a comment.