Question

Determine whether the system has no solutions, one solution or infinitely many solutions.

Answer 1

Infinitely many solutions

Step-by-step explanation

`\begin{gathered} -3x-5y+36z=40\Rightarrow equation(1) \\ -x+7z=5\Rightarrow equation(2) \\ x+y-10z=-10\Rightarrow equation(3) \end{gathered}`

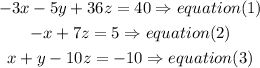
Step 1

in order to get a new equation with only x and z

a) multiply equation (3) by 5 and add the new equation to equation (1)

`\begin{gathered} x+y-10z=-10\Rightarrow equation(3) \\ \text{Multiplied by 5} \\ 5x+5y-50z=-50 \\ \text{add equation (1)} \\ 5x+5y-50z=-50 \\ -3x-5y+36z=40\Rightarrow equation(1) \\ _(------------------) \\ 2x-14z=-10\Rightarrow equation(4) \end{gathered}`

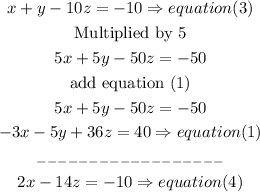
b) now use equations ( 2) and (4) to find x and z

`\begin{gathered} 2x-14z=-10\Rightarrow equation(4) \\ -x+7z=5\Rightarrow equation(2) \end{gathered}`

isolate x in both sides, then set equal

`\begin{gathered} 2x-14z=-10\Rightarrow equation(4) \\ 2x=-10+14z \\ x=(-10+14z)/(2) \\ -x+7z=5\Rightarrow equation(2) \\ 7z-5=x \\ x=7z-5 \end{gathered}`

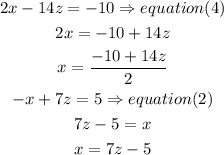
x= x, so

`\begin{gathered} x=x \\ (-10+14z)/(2)=7x-5 \\ solve\text{ for z} \\ -10+14z=2(7z-10) \\ -10+14z=14z-10 \\ -10+10=14z-14z \\ 0=0 \end{gathered}`

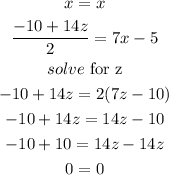
when we end with 0=0 , then it means that the left-hand side and the right-hand side of the equation are equal to each other regardless of the values of the variables involved; therefore, its solution set is all real numbers for each variable

therefore, the answer is

Infinitely many solutions

I hope this helps you