Recalling the formula for calculating the area of a rectangle:
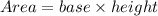
Since the base is equal to (x+6) meters and the height is equal to (2x-1) (it actually doesn't matter which is the height and which is the base), then:
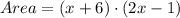
Use the distributive property two times to rewrite the expression in terms of x:
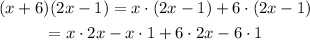
Use additional properties of multiplication and addition to further simplify the expression:
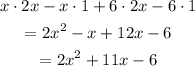
Therefore, the area of the rectangle is 2x^2+11x-6 square meters.