Solution:
Given:
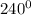
To get sin 240 degrees:
240 degrees falls in the third quadrant.
In the third quadrant, only tangent is positive. Hence, sin 240 will be negative.
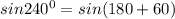
Using the trigonometric identity;
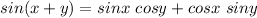
Hence,

To get cos 240 degrees:
240 degrees falls in the third quadrant.
In the third quadrant, only tangent is positive. Hence, cos 240 will be negative.
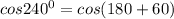
Using the trigonometric identity;
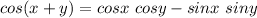
Hence,

To get tan 240 degrees:
240 degrees falls in the third quadrant.
In the third quadrant, only tangent is positive. Hence, tan 240 will be positive.
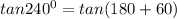
Using the trigonometric identity;
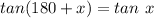
Hence,
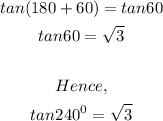
To get cosec 240 degrees:

To get sec 240 degrees:
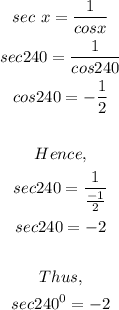
To get cot 240 degrees:
