Answer
The perimeter of the trapezium is 111.46 units
Solution
- We are given the image of a trapezium with a lower base of RG = 43, a slant height of IG = 18√2, and an angle of 45° subtended by the slant height with the base of the trapezium.
- We are asked to find the perimeter of the trapezium. This simply requires that we add up all the lengths that make up the trapezium together. That is:
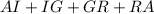
- Since the figure given is a trapezium, lengths RA = IT because lengths AI and RT are parallel lines. This means we can update our formula above as:
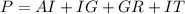
- The lengths GR and IG are known. Lengths AI and IT are not known. To get both lengths, we simply need to consider ∆ITG.
- We can use SOHCAHTOA to get the lengths of IT and TG in the triangle. To get the length AI, we can observe that AI = RT and RT + TG = GR.
- Thus, we can say:
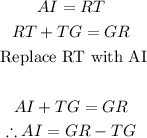
- With the above explanation, we can proceed to solve the question.
Finding IT and TG:
![\begin{gathered} \text{ Using SOHCAHTOA:} \\ \sin 45=\frac{IT}{18\sqrt[]{2}} \\ \therefore IT=18\sqrt[]{2}*\sin 45 \\ IT=18 \\ \\ \cos 45=\frac{TG}{18\sqrt[]{2}} \\ \therefore TG=18\sqrt[]{2}*\cos 45 \\ TG=18 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/g4kz0wekvnyqzejn0cbr6qy5f65sy2inwn.png)
- Thus, IT = 18 and TG = 18.
Finding AI:
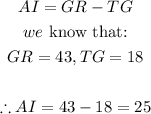
- Thus, AI = 25
- Now, we can proceed to calculate the Perimeter of the trapezium as follows:
![\begin{gathered} P=AI+IG+GR+IT \\ P=25+18\sqrt[]{2}+43+18 \\ P=86+18\sqrt[]{2} \\ \therefore P\approx111.46\text{ (To the nearest hundredth)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/566yxwojv1scxow98kxox6sdzvbexo2db0.png)
Final Answer
The perimeter of the trapezium is 111.46 units