Given data:
The length of the rectangle is l=(3x+5) .
The width of the rectangle is b= (2x-2).
The expression for the perimeter is,

Substitute the given values in the above expression.
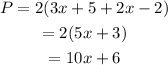
The expression for the area is,

Substitute the given values in the above expression.
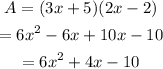
Thus, the perimeter is 10x+6, and the area is 6x^(2) +4x-10.