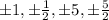The given polynomial function is:

Since all the co-efficients are integers, we can apply the rational zero theorem.
The trailing co-efficient ( the co-efficient of the constant term) is 5.
Find its factors with the plus and minus sign; thus we have;

The leading co-efficient ( the co-efficient of the term with the highest degree) is 2.
Find its factors with the plus and minus sign; thus we have:
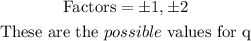
Next, is finding all possible values for the rational expression p/q. Thus, we have:

Hence, the possible rational zeros for the polynomial function are: