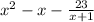Question

Rewrite the given rational expression in the form q(x) + r(x)/b(x) where q(x) = quotient, r(x) = remainder, and b(x) = divisor. (x3 – x – 23)/(x + 1)

Answer 1

Use long division to find the quotient:

`(x^3-x-23)/(x+1)`

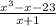
The procedure of the long division is shown:

As we can see, the quotient is x²-x, with a remainder of -23 when the divisor is x+1.

Therefore, we can rewrite the rational expression as:

`(x^3-x-23)/(x+1)=x^2-x-(23)/(x+1)`

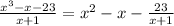
Where:

`\begin{gathered} q(x)=x^2-x \\ b(x)=x+1 \\ r(x)=-23 \end{gathered}`

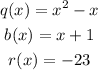
Therefore, the answer is:

`x^2-x-(23)/(x+1)`