The Solution:
Given:
We are required to find the volume of the box only.
By formula, the volume of the box is:
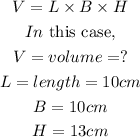
Substitute these values in the formula.
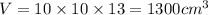
Thus, the volume of the rectangular prism only is 1300 cubic centimeters
The second part of the question is to find the volume of the box with the bowl-shaped head out.
The radius of the hemisphere is:
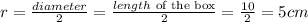
The volume of a hemisphere is:
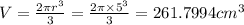
The volume of the box with the bowl-shaped head out is:
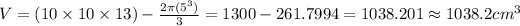
Thus, the correct answer is 1038.2 cubic centimeters.