Question

Determine number of intersection if they exist, determine the point of intersection. Only for ii)

Answer 1

Step-by-step explanation

In this problem, we have to:

• a) determine the number of intersections between two functions,

,

• b) find the points of intersection.

The discriminant of a polynomial y = ax² + bx + c is given by:

`\Delta=b^2-4ac.`

According to the value of the discriminant, we have:

• for Δ > 0 ⇒ two solutions,

,

• for Δ = 0 ⇒ one solution,

,

• for Δ < 0 ⇒ no solutions.

The solutions for y = 0 are given by:

`x=(-b\pm√(\Delta))/(2a).`

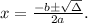
ii) We have the functions:

`\begin{gathered} f(x)=5x^2-x+1, \\ g(x)=2x+3. \end{gathered}`

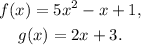
(a) At the intersection of the functions, we have:

`\begin{gathered} f(x)=g(x), \\ 5x^2-x+1=2x+3, \\ 5x^2-3x-2=0. \end{gathered}`

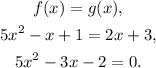
Comparing this polynomial with the general equation from above, we see that:

• a = 5,

,

• b = -3,

,

• c = -2.

To find the number of intersections, we compute the discriminant of this polynomial:

`\Delta=(-3)^2-4\cdot5\cdot(-2)=9+40=49>0\Rightarrow\text{ two solutions.}`

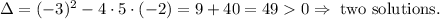
So we have two intersections.

(b) The values of x at the intersections are:

`x=(-(-3)\pm√(49))/(2\cdot5)=(3\pm7)/(10)\Rightarrow\begin{cases}x_1=\text{ }{1} \\ x_2={-(2)/(5)}.\end{cases}`

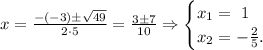
Replacing these values in the equation of one of the polynomials, we get:

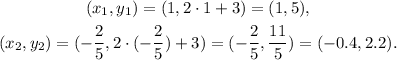
`\begin{gathered} (x_1,y_1)=(1,2\cdot1+3)=(1,5), \\ (x_2,y_2)=(-(2)/(5),2\cdot(-(2)/(5))+3)=(-(2)/(5),(11)/(5))=(-0.4,2.2). \end{gathered}`Answer

(ii)

• (a) There are 2 intersections

,

• (b) The intersections are (1,5) and (-0.4, 2.2)