The figure given is a prism with five surfaces. It comprises of two triangluar surfaces and three rectangular surfaces. The two triangles are of equal dimensions, while the remaining three rectangles are of different dimensions
The triangles has the base and perpendicular height as
![\begin{gathered} \text{base}=10\operatorname{cm} \\ \text{height}=4\operatorname{cm} \end{gathered}]()
The dimensions of the rectangles are
![\begin{gathered} \text{The first rectangle with dimension} \\ \text{length}=L_1=10\operatorname{cm} \\ \text{width}=W_1=9\operatorname{cm} \\ \text{The second rectangle with dimension} \\ length=L_2=5\operatorname{cm} \\ \text{width}=W_2=9\operatorname{cm} \\ \text{The third rectangle with dimension} \\ \text{length}=L_3=8\operatorname{cm} \\ \text{width}=W_3=9\operatorname{cm} \end{gathered}]()
The area of a triangle is given by the formula
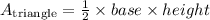
The area of a rectangle is given by the formula
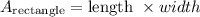
The total surface area of the given figure is
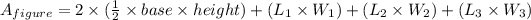
![\begin{gathered} A_{\text{figure}}=2*((1)/(2)*10*4)+(10*9)+(5*9)+(8*9) \\ A_{\text{figure}}=40+90+45+72 \\ A_{\text{figure}}=247\operatorname{cm}^2 \end{gathered}]()
Hence, the surface area of the given figure is 247cm²