Question

Using the properties, complete each equation and solve for the variable.-equation is in the photo

Answer 1

Hello!

Let's remember the property of multiplication of two equal values with0 different exponents:

We'll have to keep the base and add the exponents.

Now, let's try to solve your exercise:

`x^(12)\cdot x^n=x^(12+n)`

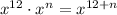
What value when added to 12, results in 12?

Just 0, right? Because 12 + 0 = 12

So, let's replace it in the equation:

`\begin{gathered} x^(12)\cdot x^0=x^(12+0) \\ x^(12)_{}\cdot1=x^(12) \end{gathered}`

Also, you must remember that any number when elevated to exponent 0, equals 1, so x^12 * 1 = x^12.

In this exercise, the value of N is 0.