The function can be described as:
It is the line v(t)=6 from 0 to 3.
From t=3 to t=4, it is a line that passes through (3,6) and (4,0)
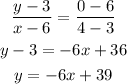
So v(t)=-6t+39 from 3 to 4
From 4 to 6 it passes through (0,4) and (6,-2)

v(t)=-t+4 from 4 to 6
From 6 to 7 the line passes through (6,-2) and (7,0) so the equation will be:
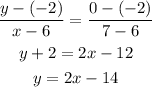
So v(t)=2t-14 from 6 to 7.
So the displacement from 0 to 7 is given by:
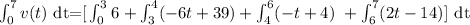
Integrate to get:
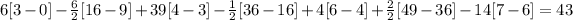
So the displacement is 43 units.