Question

An athele sprint 100 m to the right in 10 s, stops for 3 s and then walks back to the starting line in 25 s. Determine a) the average velocity for the sprint b.) the average velocity for the walk c.) the average velocity and average speed of the entire round trip.I am not sure how to break this problem down to help my son. Could you please help

Answer 1

Let's make a diagram to visualize the situation.

As you can observe in the diagram above, the distance is 100 meters. To find the average velocity for the sprint, we have to divide the distance by the time.

`\begin{gathered} \bar{v_{\text{sprint}}}=(100m)/(10\sec) \\ \bar{v_{}}=10((m)/(s)) \end{gathered}`

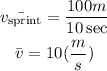
(a) The average velocity for the sprint is 10 meters per second.

We know that the athlete takes 25 seconds to walk back the 100 meters. Let's divide again to find the average velocity for the walk.

`\begin{gathered} v_{\text{walk}}=(-100m)/(25\sec ) \\ v_{\text{walk}}=-4((m)/(s)) \end{gathered}`

(b) The average velocity for the walk is -4 meters per second. Observe that this velocity is negative, that is because the athlete is going in the opposite direction (left side).

To find the average velocity we have to divide the total displacement by the total time spent. However, the total displacement, in this case, is zero because the athlete is going back to the starting point.

`v=(0m)/(10\sec +25\sec )=0((m)/(s))`

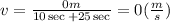
Therefore, the average velocity is zero for the entire round trip.

To find the average speed, we have to divide the total distance travel by the time spent.

`\begin{gathered} \bar{v}=(200m)/(10\sec+25\sec)=(200m)/(35\sec ) \\ \bar{v}\approx5.71((m)/(s)) \end{gathered}`

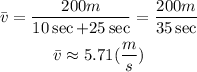
Therefore, the average speed is 5.71 meters per second.