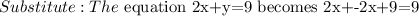Solution:
Given the system of equations:
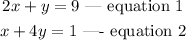
To solve,
Step 1: From equation 1, solve for y.
To solve for y, we make y the subject of the equation.
Thus,

Step 2: Substitute equation 3 into equation 2, to solve for x.
Thus,
![\begin{gathered} x+4y=1 \\ \Rightarrow x+4(-2x+9)=1 \\ open\text{ parentheses,} \\ x-8x+36=1 \\ \Rightarrow-7x+36=1 \\ subtract\text{ 36 from both sides of the equation,} \\ -7x+36-36=1-36 \\ \Rightarrow-7x=-35 \\ divide\text{ both sides by the coefficient of x, which is -7} \\ -(7x)/(-7)=-(35)/(-7) \\ \Rightarrow x=5 \end{gathered}]()
Step 3: To solve for y, substitute the value of 5 for x into equation 3.
From equation 3,
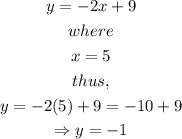
Hence, the step that contains the first error is