Question

Find the sector area that is shaded in yellow and the arc length traced in red in the circle below.

Answer 1

The question provides the following parameters for the sector under consideration:

`\begin{gathered} \theta=60\degree \\ r=14\text{ in} \end{gathered}`

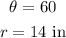
PART A: Arc Length

The formula to calculate the Arc Length is given as

`L=(\theta)/(360)*2\pi r`

Therefore, we can substitute the values for the parameters and solve as

`\begin{gathered} L=(60)/(360)*2*\pi*14 \\ L=(1)/(6)*28\pi \\ L=14.66\approx14.7in \end{gathered}`

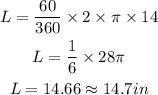
The arc length is 14.7 inches.

PART B: Sector Area

The formula to calculate the Arc Length is given as

`A=(\theta)/(360)*\pi r^2`

Therefore, we can substitute the values and solve as

`\begin{gathered} A=(60)/(360)*\pi*14^2 \\ A=(1)/(6)*196\pi \\ A=102.6in^2 \end{gathered}`

The sector area is 102.6 square inches.